伸展树
在上一篇博文中提到的伸展树(splay tree).其实自己也没怎么明白.在网上找了半天也没有看懂.最终找到了这个.这是加州大学伯克利分校的CS 61B数据结构的一个公开课视频.讲的清楚极了.现部分整理如下.
一.伸展树是一种平衡二叉搜索树.它可以快速的获得最近操作的项目.对于伸展树.最基本的策略是旋转(Rotation).旋转分为左旋和右旋.如下:

二.伸展树的基本操作:
1.查找(K):和普通的二叉树没什么区别.然后让查找结束的节点X成为根(splay)(不管是否找到目标K.)

2.伸展(splay X):有三种情况.
-
Zig-zag:
X是一个右节点的左节点.或者X是一个左节点的右节点.
旋转X两次.

-
Zig-zig:
X是一个左节点的左节点.或者X是一个右节点的右节点.
旋转两次.但和Zig-zag的旋转顺序有差异.先旋转X的父节点.在旋转X.

-
Zig:
X是根的子节点.
那么就是一次旋转

Zig-zag和Zig-zig都是对两层深度的操作.直到X成为根的子节点.就进行Zig操作.
下面是一个查找的例子.

首先.象普通的二叉搜索树一样.找到7.可见.7是一个右节点的右节点.那么就进行Zig-zig步骤.此时7是一个右节点的左节点.就进行Zig-zag步骤.再进行一个Zig步骤.一个查找7的操作就完成了.
3.插入(K):首先象普通的二叉搜索树一样将K插入.再将K伸展至根.
4.删除(K):象普通的二叉搜索树一样将K删除.然后将K的父节点X伸展至根.如果K没有在树内的话.那么就如同查找操作.即将最后一个访问的节点伸展至根.

这里有一个在线的示例:http://www.ibr.cs.tu-bs.de/courses/ss98/audii/applets/BST/SplayTree-Example.html
另一小段功能不全的测试代码..只能打印树的深度...(摊手)(摇头)
def inorder():
d=dict()
def inner_inorder(n,r):
if n is None :
return
else:
inner_inorder(n.left,r=r+1)
if d.get(r) is None:
d[r]=[n.key]
else:
d[r].append(n.key)
inner_inorder(n.right,r=r+1)
inner_inorder(t.root,0)
return d
def print_tree():
d=inorder()
for i in d:
print "%s"%d[i]
t=SplayTree()
for i in range(9):
t.insert(i)
print_tree(t)
利用coverage测试python代码覆盖率
主程序是一个伸展树(Splay Tree).如下(链接):
class Node:
def __init__(self, key):
self.key = key
self.left = self.right = None
def equals(self, node):
return self.key == node.key
class SplayTree:
def __init__(self):
self.root = None
self.header = Node(None) #For splay()
def insert(self, key):
if (self.root == None):
self.root = Node(key)
return
self.splay(key)
if self.root.key == key:
# If the key is already there in the tree, don't do anything.
return
n = Node(key)
if key < self.root.key:
n.left = self.root.left
n.right = self.root
self.root.left = None
else:
n.right = self.root.right
n.left = self.root
self.root.right = None
self.root = n
def remove(self, key):
self.splay(key)
if key != self.root.key:
raise 'key not found in tree'
# Now delete the root.
if self.root.left== None:
self.root = self.root.right
else:
x = self.root.right
self.root = self.root.left
self.splay(key)
self.root.right = x
def findMin(self):
if self.root == None:
return None
x = self.root
while x.left != None:
x = x.left
self.splay(x.key)
return x.key
def findMax(self):
if self.root == None:
return None
x = self.root
while (x.right != None):
x = x.right
self.splay(x.key)
return x.key
def find(self, key):
if self.root == None:
return None
self.splay(key)
if self.root.key != key:
return None
return self.root.key
def isEmpty(self):
return self.root == None
def splay(self, key):
l = r = self.header
t = self.root
self.header.left = self.header.right = None
while True:
if key < t.key:
if t.left == None:
break
if key < t.left.key:
y = t.left
t.left = y.right
y.right = t
t = y
if t.left == None:
break
r.left = t
r = t
t = t.left
elif key > t.key:
if t.right == None:
break
if key > t.right.key:
y = t.right
t.right = y.left
y.left = t
t = y
if t.right == None:
break
l.right = t
l = t
t = t.right
else:
break
l.right = t.left
r.left = t.right
t.left = self.header.right
t.right = self.header.left
self.root = t
测试如下(链接):
import unittest
from splay import SplayTree
class TestCase(unittest.TestCase):
def setUp(self):
self.keys = [0, 1, 2, 3, 4, 5, 6, 7, 8, 9]
self.t = SplayTree()
for key in self.keys:
self.t.insert(key)
def testInsert(self):
for key in self.keys:
self.assertEquals(key, self.t.find(key))
def testRemove(self):
for key in self.keys:
self.t.remove(key)
self.assertEquals(self.t.find(key), None)
def testLargeInserts(self):
t = SplayTree()
nums = 40000
gap = 307
i = gap
while i != 0:
t.insert(i)
i = (i + gap) % nums
def testIsEmpty(self):
self.assertFalse(self.t.isEmpty())
t = SplayTree()
self.assertTrue(t.isEmpty())
def testMinMax(self):
self.assertEquals(self.t.findMin(), 0)
self.assertEquals(self.t.findMax(), 9)
if __name__ == "__main__":
unittest.main()
运行:
(rrandom)-(~/python-codes/udacity/RegehrCS258)-(07:27 下午 六 10月 06) -> py splayTest.py ..... ---------------------------------------------------------------------- Ran 5 tests in 1.454s OK
但是否每一行代码都运行过了呢?代码覆盖律(code coverage)就是指测试中代码的运行的程度.如果代码覆盖律小于100%.那就意味着还有语句没有被执行.这时候就要coverage出场了.
(rrandom)-(~/python-codes/udacity/RegehrCS258)-(07:42 下午 六 10月 06) -> coverage erase;coverage run splayTest.py; ..... ---------------------------------------------------------------------- Ran 5 tests in 2.294s OK
erase是清空上次的数据.coverage 还可以生成html,方便查看
(rrandom)-(~/python-codes/udacity/RegehrCS258)-(07:50 下午 六 10月 06) -> coverage erase;coverage run splayTest.py;coverage html -i ..... ---------------------------------------------------------------------- Ran 5 tests in 2.298s OK
得到结果:
Coverage report: 93%
| Module | statements | missing | excluded | coverage |
|---|---|---|---|---|
| Total | 130 | 9 | 0 | 93% |
| splay | 98 | 9 | 0 | 91% |
| splayTest | 32 | 0 | 0 | 100% |
查看详细.是那些语句没有被执行:
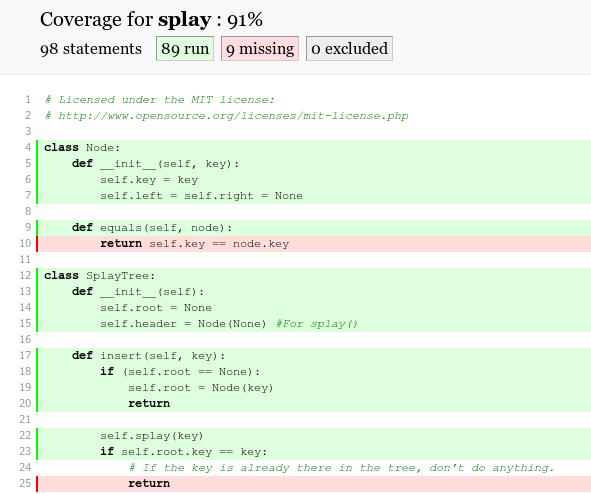
excluded表示你告诉coverage忽略的代码.
现在尝试修改测试代码.删除一个不在树里的节点:
def testRemove(self):
for key in self.keys:
self.t.remove(key)
self.assertEquals(self.t.find(key), None)
self.t.remove(-999)
再次运行coverage:
(rrandom)-(~/python-codes/udacity/RegehrCS258)-(07:50 下午 六 10月 06)
-> coverage erase;coverage run splayTest.py;coverage html -i
....E
======================================================================
ERROR: testRemove (__main__.TestCase)
----------------------------------------------------------------------
Traceback (most recent call last):
File "splayTest.py", line 22, in testRemove
self.t.remove(-999)
File "/home/rrandom/python-codes/udacity/RegehrCS258/splay.py", line 39, in remove
self.splay(key)
File "/home/rrandom/python-codes/udacity/RegehrCS258/splay.py", line 86, in splay
if key < t.key:
AttributeError: 'NoneType' object has no attribute 'key'
----------------------------------------------------------------------
Ran 5 tests in 2.382s
FAILED (errors=1)
这是一个不在预期内的错误.但是这一行却没有被执行.

那么错误应该在self.splay(key)内.
[scheme学习笔记]二叉树的遍历
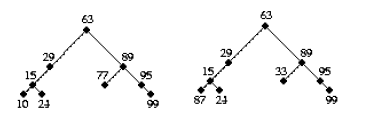
(define BT1 (make-node 63 'a
(make-node 29 'b
(make-node 15 'c
(make-node 10 'd false false)
(make-node 24 'e false false)) false)
(make-node 89 'f
(make-node 77 'g false false)
(make-node 95 'h false
(make-node 99 'i false false)))))
(define BT2 (make-node 63 'a
(make-node 29 'b
(make-node 15 'c
(make-node 87 'd false false)
(make-node 24 'e false false)) false)
(make-node 89 'f
(make-node 33 'g false false)
(make-node 95 'h false
(make-node 99 'i false false)))))

;;inorder:BT->list
(define (inorder BT)
(cond
((boolean? BT) empty)
(else
(append
(inorder (node-left BT))
(list (node-ssn BT))
(inorder (node-right BT))))))
(define (preorder BT)
(cond
((boolean? BT) empty)
(else
(append
(list(node-ssn BT))
(preorder (node-left BT))
(preorder (node-right BT))))))
(define (postorder BT)
(cond
((boolean? BT) empty)
(else
(append
(postorder (node-left BT))
(postorder (node-right BT))
(list(node-ssn BT))))))