深度优先搜索和广度优先搜索(非递归).
深度优先:
- 将openlist中的最后一项取出.
-
将其未标记的邻项标记为已访问.并放入openlist.
-
重复此步骤1.2.直到openlist为空.
例:
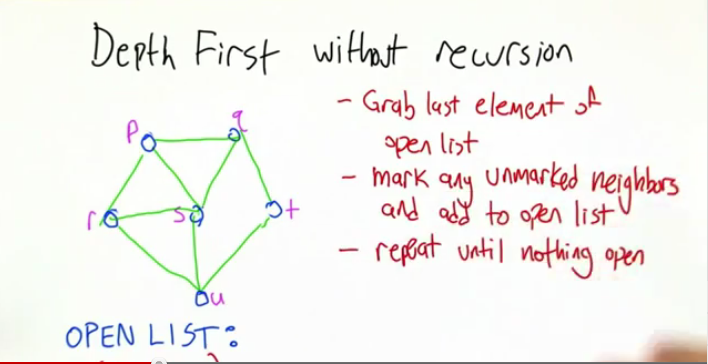
上图中图从P开始,openlist:
[p] [r,s,q] [r,s,t] [r,s,u] [r,s] [r] []
广度优先则是将openlist中的第一项取出.有:
[p] [r,s,q] [s,q,u] [q,u] [u,t] [t] []
Grabbing the last element means you are using a "stack". Grabbing the first means you are using a "queue". -MLL
深度优先使用的是栈.广度优先使用的是队列.
[scheme学习笔记]二叉树的遍历
将二叉树的节点定义为
(define-struct node (number value left right))
则树的定义数据定义是
binary-tree（简称BT）是下列两者之一
1． false；
2． (make-node num value lft rgt)，
其中 num是数，value是符号，lft 和rgt 是BT。
则如图的二叉树可以表示为
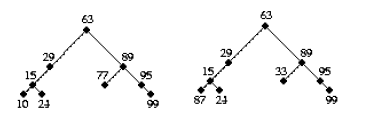
(define BT1 (make-node 63 'a
(make-node 29 'b
(make-node 15 'c
(make-node 10 'd false false)
(make-node 24 'e false false)) false)
(make-node 89 'f
(make-node 77 'g false false)
(make-node 95 'h false
(make-node 99 'i false false)))))
(define BT2 (make-node 63 'a
(make-node 29 'b
(make-node 15 'c
(make-node 87 'd false false)
(make-node 24 'e false false)) false)
(make-node 89 'f
(make-node 33 'g false false)
(make-node 95 'h false
(make-node 99 'i false false)))))
如果从左到右读出这两棵树中的数.可以得到两个序列
其中数A是按照升序排列的.将有序排列的二叉树称为二叉搜索树.
接下来开发函数inorder.中序遍历.该函数读入一棵二叉树，返回树中所有number数组成的表。该表以
从左到右的顺序（上图顺序）列出这些数.
;;inorder:BT->list
(define (inorder BT)
(cond
((boolean? BT) empty)
(else
(append
(inorder (node-left BT))
(list (node-ssn BT))
(inorder (node-right BT))))))
中序遍历按照左根右的顺序进行历遍.即首先遍历左子树,然后访问根结点,最后遍历右子树.在遍历左,右子树时.仍然先遍历左子树,再访问根结点,最后遍历右子树
而前序遍历按照根左右的顺序进行遍历.
后续遍历按照左右根的顺序进行遍历.
同理即可得到前序遍历和后续遍历的函数.
(define (preorder BT)
(cond
((boolean? BT) empty)
(else
(append
(list(node-ssn BT))
(preorder (node-left BT))
(preorder (node-right BT))))))
(define (postorder BT)
(cond
((boolean? BT) empty)
(else
(append
(postorder (node-left BT))
(postorder (node-right BT))
(list(node-ssn BT))))))
可以发现对二叉搜索树来说.中序遍历返回的是有序排列的表.
ps.写个博客都要翻墙.蛋疼死啊..
ps2.用递归的函数写递归的数据结构真是太清晰了.感觉就是C语言写出来是个麻烦的东西.指针满天飞..
[scheme学习笔记]scheme中的快速排序和合并排序
快速排序:
快速排序是分而治之思想的体现,即将非平凡可解的问题分成相关的两个小问题.分别解决这两个小问题.再将所得结果合并起来.
具体来说.quick-sort先讲数表分成两个表.其中第一个表中所有元素小于原表中第一个元素.第二个表中元素大于等于原表中第一个元素.然后对这两个表使用同样的方法进行排序.最后再将他们连接起来.就得到了排序好的表.可设第一个元素为关键元素.
假设输入为
(list 11 8 14 7)
手工计算
关键元素:11
分成的两个表为
(list 8 7)
和
(list 14)
对第一个表使用相同方法排序.可以得到
(list 7 8)
如此.原来的表被分为三部分
1.(list 7 8)
2.11
3.(list 14)
现在将三部分合并起来,即可得到排序完成的表:
(list 7 8 11 14)
表格说明如下:
那么quick-sort就是一个递归的函数.当它遇到空表empty(即'())时停止.
先定义一个函数filter.(在racket的库中已经提供.).用于选出一个表中是某个函数为真的所有元素.此判定函数依次作用于表中所有函数.
;;filter:listX-listX
(define (filter pred list)
(cond
((empty? list) list)
(else (cond
((pred (car list))
(cons (car list) (filter pred (cdr list))))
(else (pred (cdr list)))))))
运用filter.可以写出分开两个表的表达式.
那么.quick-sort可以定义了
(define (q-sort lst)
(if (null? lst)
lst
(append (q-sort (filter (lambda (x) (<= x (car lst))) (cdr lst)))
(list (car lst))
(q-sort (filter (lambda (x) (> x (car lst))) (cdr lst))))))
归并排序:
这个我也没理解透.只是按照how to design programs 习题 26.1.2一步步做出来的.
先抄题.
习题 26.1.2 开发函数 merge-sort，对数表排序（升序排列），使用如下两个辅助函数：
1． 第一个辅助函数 make-singles，它使用给定的表中的数构造一个单元素表的表。例如，
(equal? (make-singles (list 2 5 9 3))
(list (list 2) (list 5) (list 9) (list 3)))
2． 第二个辅助函数merge-all-neighbors，它合并相邻的两个表。更精确地说，它读入一个（数）表
的表，合并相邻的表。例如，
(equal? (merge-all-neighbors (list (list 2) (list 5) (list 9) (list 3)))
(list (list 2 5) (list 3 9)))
(equal? (merge-all-neighbors (list (list 2 5) (list 3 9)))
(list (list 2 3 5 9)))
一般来说，这个函数生成一个大概是输入表一半长的表。为什么输出的表并不总是输入表的一半
长？
确保这两个函数的开发相互独立。
函数 merge-sort 首先使用make-singles 把输入表分割为由单元素表组成的表；然后不断地使用
merge-all-neighbors 合并表，并且每次都使用sort 函数对每个小表排序，直至最终得到单一的表；最后这个
表就是merge-sort 的返回值。
代码如下.
;;merge-sort:list->list
(define (merge-sort x)
(define (merge-sort-worker x)
(if (= (length x) 1)
(car x)
(merge-sort-worker (merge-all-neighbors x))))
(merge-sort-worker (make-singles x)))
;;make-singles:alon-> lists of number
(define (make-singles alon)
(cond
((empty? alon) empty)
(else (cons(cons (first alon) empty) (make-singles (rest alon))))))
;;merge-all-neighbors:lists->list
(define (merge-all-neighbors alist)
(cond
((empty? alist) empty)
((empty? (rest alist)) empty)
(else (cons (sort (append (first alist)(second alist))<)(merge-all-neighbors (rest (rest alist)))))))
另..
how to design programs中文版下载地址
ftp://ftp.cs.sjtu.edu.cn:990/huanglp/程序设计方法/如何设计程序.PDF
[scheme学习笔记]递归插入排序
对数表进行排序,排序函数读入一个表,产生另一个表
即
;; sort : list-of-numbers -> list-of-numbers ;; to create a sorted list of numbers from all the numbers in alon (define (sort alon) ...)
例子为:
(sort empty) ;; expected value: empty (sort (cons 1297.04 (cons 20000.00 (cons -505.25 empty)))) ;; expected value: (cons 20000.00 (cons 1297.04 (cons -505.25 empty)))
如果输入为empty.则输出empty
因为sort是递归定义的.所以可以得出函数的模板为:
(define (sort alon)
(cond
((empty? alon)empty)
(else (...(first alon)...(sort (rest alon))))))
接着,需要处理的就是sort函数cond字句的第二部分.该部分包含两个表达式.先弄清楚他们结果分别是什么.
1.(first alon)输出数表的第一个数
2.(sort(rest alon))是对数表的剩下部分进行排序的结果
则可以知道.这个字句需要做的就是将(first alon)插入到表(sort(rest alon))中.
要讲数插入表.必须历遍整个表
此处,可以定义一个函数insert,它以一个数和一个表为参数.输出一个表.
insert定义如下:
;; insert : number list-of-numbers -> list-of-numbers ;; to create a list of numbers from n and the numbers on alon ;; that is sorted in descending order; alon is already sorted (define (insert n alon) ...))
如此.就可以给出sort的定义
(define (sort alon)
(cond
((empty? alon) empty)
(else (insert (first alon) (sort (rest alon))))))
现在.cond第二个字句的意义清晰了.要产生最终值.可先取出非空表的第一个数.再对其它部分进行排序.最后把前者插入到后者的合适部分.
剩下的部分就是对insert进行设计.
首先考虑insert做什么事情.
下面是例子
第一种情况
(insert 5 empty) ;; expected value: (cons 5 empty)
如果insert的第二个参数是非空表,
则第二种情况为
(insert 1297.04 (cons 20000.00 (cons -505.25 empty))) ;; expected value: (cons 20000.00 (cons 1297.04 (cons -505.25 empty)))
可以给出函数的模板
(define (insert n alon)
(cond
((empty? alon) ...)
(else ... (first alon) ... (insert n (rest alon)) ...)))
首先给出的表达式的结果
(first alon)得到的是数表的第一个数
(insert n(rest alon))得到一个排序完成的数表
接着考虑.insert的第二个参数为非空表时,可能出现以下两种情况
1.n>=(first alon) 因为alon是一个有序表,所以alon中所有数都不不会大于n,则用cons 把n 和alon组合在一起
2.n<(first alon).即
(insert 3 (cons 6 (cons 2 (cons 1 (cons -1 empty)))))
即(first alon)是6
(insert n (rest alon))是(cons 3 (cons 2 (cons 1 (cons -1 empty))))
这样的情况时.(first alon)是最大的数.所以它排在第一位,而n要插入(rest alon)之中.
这样.得到最终结果
(cons (first alon) (insert n (rest alon)))
于是.得到完整定义:
;; sort : list-of-numbers -> list-of-numbers (sorted)
;; to create a list of numbers with the same numbers as
;; alon sorted in descending order
(define (sort alon)
(cond
[(empty? alon) empty]
[(cons? alon) (insert (first alon) (sort (rest alon)))]))
;; insert : number list-of-numbers (sorted) -> list-of-numbers (sorted)
;; to create a list of numbers from n and the numbers on
;; alon that is sorted in descending order; alon is sorted
(define (insert n alon)
(cond
[(empty? alon) (cons n empty)]
[else (cond
[(>= n (first alon)) (cons n alon)]
[(< n (first alon)) (cons (first alon) (insert n (rest alon)))])]))
