又十诫
来自The seasoned schemer
The Next Ten Commandments
The Eleventh Commandment
Use additional arguments when a function needs to know what other arguments to the function have been like so far.
The Twelfth Commandment
Use (letrec ...) to remove arguments that do not change for recursive applications.
The Thirteenth Commandment
Use(letrec ...) to hide and to protect functions.
The Fourteenth Commandment
Use(letcc1 ...) to return values abruptly and promptly.
The Fifteenth Commandment
Use (let ...) to name the values of repeated expressions in a function definition if they may be evaluated twice for one and t he same use of the function. And use (let...) to name the values of expressions(without set!) that are re-evaluated every time a function is used.
The Sixteenth Commandment
Use (set! ...)only with names defined in (let ...)s.
The Seventeenth Commandment
Use(set! x ...) for (let((x ...)) ...) only if there is at least one (lambda ... between it and the(let ...),or if the new value for x is a function that refers to x .
The Eighteenth Commandment
Use (set! x ...) only when the value that x refers to is no longer needed.
The Nineteenth Commandment
Use (set! ...) to remember valuable things between two distinct uses of a function.
The Twentieth Commandment
When thinking about a value created with (letcc ...),write down the function that is equivalent but does not forget. Then, when you use it, remember to forget.
1:letcc is call-with-current-continuation or call/cc in scheme
let,let*和letrec
在scheme中.let,let*和letrec的形式均写做:(id val-expr).即:
(let ([id val-expr] ...) body ...+),(let* ([id val-expr] ...) body ...+),(letrec ([id val-expr] ...) body ...+)
三者的不同在于,对id及val-expr的运算顺序不同.由此导致的结果也不同.
在let中.先依此所有的计算val-expr.在依此所有的计算id.
在let*中.先计算一个val-expr,将其赋值给id.在进行下一个(id val-expr)的计算.
在letrec中.id首先均为undefined.然后计算所有的val-expr.
由此:
(define foo 5) ;; foo 現在取值 5 (let ((foo 10)) ;; foo 現在取值 10 ) ;; foo 現在取值 5
这三者的区别在于,let所绑定的变量仅在它的区块内有效,而let*所绑定的变量可以在以下的绑定中使用,例如,
(let* ((var1 10) (var2 (+ var1 5))) var1) ;; 返回 15 ;; 如果僅使用 let,程式會出錯。
letrec所绑定的变量可以互相引用。因此,letrec通常被用于双重递归:
(letrec ((female (lambda(n) (if (= n 0) 1 (- n (male (female (- n 1))))))) (male (lambda(n) (if (= n 0) 0 (- n (female (male (- n 1)))))))) (display "i male(i) female(i)")(newline) (do ((i 0 (+ i 1))) ((> i 8) #f) (display i) (display " ")(display (male i))(display " ")(display (female i)) (newline)))
(via wikipedia)
同时 剥去语法糖.
(let ((x 1))
(print x))
就是
((lambda (x) (print x)) 1)
(letrec ((fact (lambda (x)
(if (= x 1)
x
(* x (fact (- x 1)))))))
(fact 5))
是
((lambda (fact x)
(fact x fact))
(lambda (x fact)
(if (= x 1)
x
(* x (fact (- x 1) fact))))
5)
也可以这样:
(letrec ((f (lambda ...))) ...)
就是
(let ((f <undefined>)) (set! f (lambda ...)) ...)
十诫
来自<the little schemer>
The First Commandment
When recurring on a list of atoms, lat, ask two questions about it: (null? lat) and else.
When recurring on a number, n, ask two questions about it: (zero? n) and else.
When recurring on a list of S-expressions, l,ask three question about it: (null? l), (atom?(car l)), and else.
The Second Commandment
Use cons to build lists.
The Third Commandment
When building a list, describe the first typical element, and then cons it onto the natural recursion.
The Fourth Commandment
Always change at least one argument while recurring.
When recurring on a list of atoms,lat,use (cdr lat).
When recurring on a num .ber, n, use (sub1 n).
And when recurring on a list of S-expressions, l, use (car l) and (cdr l) if neither (null? l) nor (atom? (car l)) are true.
It must be changed to be closer to termination. The changing argument must be tested in the termination condition:
when using test termination with cdr, test termination with null?
and when using sub1, test termination with zero?.
The Fifth Commandment
When building a value with + ,always use 0 for the value of the terminating line, for adding 0 does not change the value of an addition.
When building a value with x, always use 1 for the value of the terminating line, for multiplying by 1 does not change the value of a multiplication.
When building a value with cons, always consider '() for the value of the terminating line.
The Sixth Commandment
Simplify only after the function is correct.
The Seventh Commandment
Recur on the subparts that are of the same nature:
• On the sublists of a list.
• On the subexpressions of an arithmetic expression.
The Eighth Commandment
Use help functions to abstract from representations.
The Ninth Commandment
Abstract common patterns with a new function.
The Tenth Commandment
Build functions to collect more than one value at a time.
尾递归改写为递归
做备忘用.
上代码
#lang racket
;;factorial
;;non-tail recursion
(define (fact1 n)
(if (= 0 n)
1
(* n (fact1 (- n 1)))))
;;factorial
;;tail recursion
(define (fact-aux n result)
(if (= 0 n)
result
(fact-aux (- n 1)(* n result))))
(define (fact2 n)
(fact-aux n 1))
(define (fact3 n)
(let fact-aux ([s n][result 1])
(if (= 0 s)
result
(fact-aux (- s 1)(* s result)))))
;;fibonacci
;;non-tail recursion
(define (fib1 n)
(if (< n 2)
n
(+ (fib1 (- n 1))(fib1 (- n 2)))))
;;fibonacci
;; tail recursion
(define (fib-aux n next result)
(if (= n 0)
result
(fib-aux (- n 1) (+ next result) next)))
(define (fib2 n)
(fib-aux n 1 0))
(define (fib3 n)
(define (fib-aux n next result)
(if (= 0 n)
result
(fib-aux (- n 1) (+ next result) next)))
(fib-aux n 1 0))
when converting recursive functions to tail recursive funcion.add a auxiliary parameter.
ps. python 没有尾递归优化.
lisp系有.解释器自动将尾递归转化为迭代.
参考:
http://www.csee.umbc.edu/~chang/cs202.f98/readings/recursion.html
[scheme学习笔记]二叉树的遍历
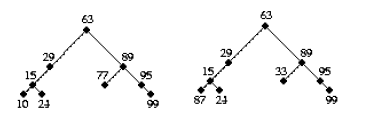
(define BT1 (make-node 63 'a
(make-node 29 'b
(make-node 15 'c
(make-node 10 'd false false)
(make-node 24 'e false false)) false)
(make-node 89 'f
(make-node 77 'g false false)
(make-node 95 'h false
(make-node 99 'i false false)))))
(define BT2 (make-node 63 'a
(make-node 29 'b
(make-node 15 'c
(make-node 87 'd false false)
(make-node 24 'e false false)) false)
(make-node 89 'f
(make-node 33 'g false false)
(make-node 95 'h false
(make-node 99 'i false false)))))

;;inorder:BT->list
(define (inorder BT)
(cond
((boolean? BT) empty)
(else
(append
(inorder (node-left BT))
(list (node-ssn BT))
(inorder (node-right BT))))))
(define (preorder BT)
(cond
((boolean? BT) empty)
(else
(append
(list(node-ssn BT))
(preorder (node-left BT))
(preorder (node-right BT))))))
(define (postorder BT)
(cond
((boolean? BT) empty)
(else
(append
(postorder (node-left BT))
(postorder (node-right BT))
(list(node-ssn BT))))))