The Way 2 Inner Peace.

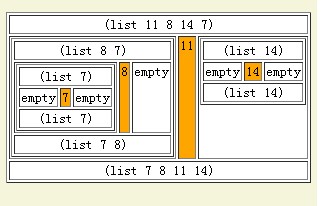
;;filter:listX-listX
(define (filter pred list)
  (cond
    ((empty? list) list)
    (else (cond
          ((pred (car list))
           (cons (car list) (filter pred (cdr list))))
          (else (pred (cdr list)))))))

(define (q-sort lst)
  (if (null? lst)
      lst
      (append (q-sort (filter (lambda (x) (<= x (car lst))) (cdr lst)))
              (list (car lst))
              (q-sort (filter (lambda (x) (> x (car lst))) (cdr lst))))))

;;merge-sort:list->list
(define (merge-sort x)
  (define (merge-sort-worker x)
    (if (= (length x) 1)
        (car x)
        (merge-sort-worker (merge-all-neighbors x))))
  (merge-sort-worker (make-singles x)))

    

;;make-singles:alon-> lists of number
(define (make-singles alon)
  (cond
    ((empty? alon) empty)
    (else (cons(cons (first alon) empty) (make-singles (rest alon))))))

;;merge-all-neighbors:lists->list
(define (merge-all-neighbors alist)
  (cond
    ((empty? alist) empty)
    ((empty? (rest alist)) empty)
    (else (cons (sort (append (first alist)(second alist))<)(merge-all-neighbors (rest (rest alist)))))))

另..

how to design programs中文版下载地址

ftp://ftp.cs.sjtu.edu.cn:990/huanglp/程序设计方法/如何设计程序.PDF

原文链接:http://hi.baidu.com/pudding/blog/item/7029c8fc45c046fdfc037f2e.html

无处不在的函数

基本的函数概念

Scheme 是一门函数式语言, 因为它的函数与数据有完全平等的地位, 它可以在运行时被实时创建和修改. 也因为它的全部运行都可以用函数的方式来解释, 莫能例外.

比方说, 把 if 语句作为函数来解释? (if cond if-part else-part) 是这么一个特殊的函数: 它根据 cond 是否为真, 决定执行并返回 if-part 还是 else-part. 比如, 我可以这样写:

((if (i-am-feeling-lucky) + -) my-happyness 1)

if 函数会根据我开心与否 (i-am-feeling-lucky 是一个由我决定它的返回值的函数 :P) 返回 + 或 - 来作为对我的开心值的操作. 所谓无处不在的函数, 其意义大抵如此.

把一串操作序列当成函数呢? Scheme 是没有 "return" 的, 把一串操作序列当作一个整体, 它的返回值就是这一串序列的最后一个的返回值. 比如我们可以写

(begin (+ 1 2) (+ 3 4))

它的返回是 7.

无名的能量之源

接下来, 我们就要接触到 Scheme 的灵魂 --- Lambda. 大家可以注意到 drScheme 的图标, 那就是希腊字母 Lambda. 可以说明 Lambda 运算在 Scheme 中是多么重要.

NOTE: 这里本来应该插一点 Lambda 运算的知识的, 但是一来我自己数学就不怎么好没什么信心能讲好, 二来讲太深了也没有必要. 大家如果对 Lambda 运算的理论有兴趣的话, 可以自行 Google 相关资料.

Lambda 能够返回一个匿名的函数. 在这里需要注意两点: 第一, 我用的是 "返回" 而不是 "定义". 因为 Lambda 同样可以看成一个函数 --- 一个能够生成函数的函数. 第二, 它是匿名的, 意思是, 一个函数并不一定需要与一个名字绑定在一起, 我们有时侯需要这么干, 但也有很多时候不需要.

我们可以看一个 Lambda 函数的基本例子:

((lambda (x y) (+ x y)) 1 2)

这里描述了一个加法函数的生成和使用. (lambda (x y) (+ x y)) 中, lambda 的第一个参数说明了参数列表, 之后的描述了函数的行为. 这就生成了一个函数 , 我们再将 1 和 2 作用在这个函数上, 自然能得到结果 3.

我们先引入一个 define 的操作, define 的作用是将一个符号与一个对象绑定起来. 比如 (define name 'kyhpudding) 之后再敲入 name, 这时候 Scheme 解释器就知道如何处理它了, 它会返回一个 kyhpudding.

我们自然也可以用 define 把一个符号和函数绑定在一起, 就得到了我们常用的有名函数.

(define add
        (lambda (x y) (+ x y)))

做一个简单的替换, 上面的例子就可以写成 (add 1 2), 这样就好理解多了.

上面的写法有点晦涩, 而我们经常用到的是有名函数, 所以我们有一个简单的写法, 我们把这一类简化的写法叫 "语法糖衣". 在前面我们也遇到一例, 将 (quote x) 写成 'x 的例子. 上面的定义, 我们可以这样写

(define (add x y) (+ x y))

Lambda 运算有极其强大的能力, 上面只不过是用它来做传统的 "定义函数" 的工作. 它的能力远不止如此. 这里只是举几个小小的例子:

我们经常会需要一些用于迭代的函数, 比如这个:

(define (inc x) (+ x 1))

我们也需要减的, 乘的, 还有其他各种乱七八糟的操作, 我们需要每次迭代不是 1, 而是 2, 等等等等. 我们很自然地有这个想法: 我们写个函数来生成这类迭代函数如何? 在 Scheme 中, 利用 lambda 运算, 这是可行且非常简单的. 因为在 Scheme 中, 函数跟普通对象是有同样地位的, 而 "定义" 函数的 lambda, 其实是能够动态地为我们创造并返回函数对象的. 所以我们可以这么写:

(define (make-iterator method step)
        (lambda (x) (method x step)))

没有语法糖衣的写法是:

(define make-iterator
        (lambda (method step)
                (lambda (x) (method x step))))

这个简单的例子, 已经能够完成我们在 C 之类的语言无法完成的事情. 要生成上面的 inc 函数, 我们可以这么写:

(define inc (make-iterator + 1))

这个例子展示的是 Scheme 利用 Lambda 运算得到的能力. 利用它, 我们可以写出制造函数的函数, 或者说制造机器的机器, 这极大地扩展了这门语言的能力 . 我们在以后会有更复杂的例子.

接下来, 我们会介绍 Scheme 的一些语言特性是怎么用 Lambda 运算实现的 --- 说Scheme 的整个机制是由 Lambda 驱动的也不为过.

比如, 在 Scheme 中我们可以在任何地方定义 "局部变量", 我们可以这么写:

(let ((x 1) (y 2)) 运用这些局部变量的语句)

其实 let 也只不过是语法糖衣而已, 因为上面的写法等价于:

((lambda (x y)
         运用这些局部变量的语句)
 1 2)

一些常用的函数

虽然说这篇文章不太注重语言的实用性. 但这里还是列出我们经常用到的一些操作,这能极大地方便我们的编程, 大家也可以想想他们是怎么实现的.


- cond

相当于 C 中的 switch

(cond
 (条件1 执行体)
 (条件2 执行体)
 (else 执行体))

- 循环语句

没有循环语句...... 至少没有必要的循环语句. Scheme 认为, 任何的循环迭代都
可以用递归来实现. 我们也不用担心递归会把栈占满, 因为 Scheme 会自动处理尾递
归的情况. 一个简单的 0 到 10 迭代可以写成这样.

(define (iterate x)
        (if (= x 10)
            x
            (iterate (+ x 1))))
(iterate 0)

很明显, 当我们递归调用 iterate 的时候, 我们不必保存当前的函数环境. 因为我
们递归调用完毕后就马上返回, 而不会再使用当前的环境, 这是一给尾递归的例子.
Scheme 能自动处理类似的情况甚至做一些优化, 不会浪费多余的空间, 也不会降低
效率. 所以完全可以代替循环.

当然我们有些便于循环迭代的操作, 大家可以试试自己实现他们. (当然在解释器内
部通常不会用纯 scheme 语句实现他们). 我们最常用的是 map 操作

(map (lambda (x) (+ x 1)) '(1 2 3))

运行一下这个例子, 就能理解 map 的作用了.

- 更多的数据操作

    * cadr cddr caddr 之类, 就是 car 和 cdr 的组合, 大家可以一个个试. drScheme 支持到 cadddr...
    * append: 将两个列表拼接在一起.

对数表进行排序,排序函数读入一个表,产生另一个表

即

;; sort : list-of-numbers  ->  list-of-numbers 
;; to create a sorted list of numbers from all the numbers in alon
(define (sort alon) ...)

例子为:

(sort empty)
;; expected value: 
empty

(sort (cons 1297.04 (cons 20000.00 (cons -505.25 empty))))
;; expected value: 
(cons 20000.00 (cons 1297.04 (cons -505.25 empty)))

如果输入为empty.则输出empty

(define (sort alon)
  (cond
    ((empty? alon)empty)
    (else (...(first alon)...(sort (rest alon))))))

;; insert : number list-of-numbers  ->  list-of-numbers
;; to create a list of numbers from n and the numbers on alon 
;; that is sorted in descending order; alon is already sorted
(define (insert n alon) ...))

(define (sort alon)
  (cond
    ((empty? alon) empty)
    (else (insert (first alon) (sort (rest alon))))))

现在.cond第二个字句的意义清晰了.要产生最终值.可先取出非空表的第一个数.再对其它部分进行排序.最后把前者插入到后者的合适部分.

(insert 5 empty)
;; expected value: 
(cons 5 empty)

如果insert的第二个参数是非空表,

(insert 1297.04 (cons 20000.00 (cons -505.25 empty)))
;; expected value: 
(cons 20000.00 (cons 1297.04 (cons -505.25 empty)))

(define (insert n alon)
  (cond
    ((empty? alon) ...)
    (else  ...  (first alon) ... (insert n (rest alon)) ...)))

;; sort : list-of-numbers  ->  list-of-numbers (sorted)
;; to create a list of numbers with the same numbers as
;; alon sorted in descending order
(define (sort alon)
  (cond
    [(empty? alon) empty]
    [(cons? alon) (insert (first alon) (sort (rest alon)))]))

;; insert : number list-of-numbers (sorted)  ->  list-of-numbers (sorted)
;; to create a list of numbers from n and the numbers on
;; alon that is sorted in descending order; alon is sorted
(define (insert n alon)
  (cond
    [(empty? alon) (cons n empty)]
    [else (cond
            [(>= n (first alon)) (cons n alon)]
            [(<  n (first alon)) (cons (first alon) (insert n (rest alon)))])]))